Recently I've been reading a bit of fluid dynamics, and came across the classical problem of free and forced vortices. In this post I will first discuss some mathematics leading to a computation of the free surface for the two types of vortices, and finish with a discussion of their implications.
Free vortex
A free vortex is seen in nature as either the bathtub drain or the maelstrom. A physical model of this is to start with a circular tub with a drain in the centre. To establish a steady state, refill the tub at the same rate it drains. The water is refilled near the rim of the tub, where the water enters tangential to the tub with fixed angular velocity $\omega_0$. The fluid is assumed to be incompressible and inviscid (good approximation of water) and is free of vorticity (the water is rotational on a global level, but we have a topological obstruction, so it is allowed to be locally free of vorticity). We also assume that the draining rate is slow, so that the fluid motion is dominated by rotation around the drain.
Under these conditions, the fluid can be modelled by the irrotational Euler equation \[ \frac{\partial u}{\partial t} + \nabla \left( \frac{p}{\rho} + gz + \frac{1}{2} u\cdot u\right) = 0 \] where $u$ is the fluid velocity field, $p$ is the pressure, $\rho$ is the (constant) density, $g$ is the acceleration due to gravity. We work in a cylindrical coordinate system $(r,\theta,z)$ where the $z$ axis is centred with respect to the tub, whose rim is $r = R$.
Now, by the slow-draining assumption, $u\cdot u$ is given by the square norm of the azimuthal component of the velocity. This we can determine by conservation of angular momentum: the particles come in at the rim with angular momentum $\omega_0 R^2$, so $u\cdot u = \frac{\omega_0^2 R^4}{r^2}$. In the stead-state $\partial_t u =0$, so in the end we need to have \[ \frac{1}{\rho}\frac{\partial p}{\partial z} = -g \] and \[ \frac{1}{\rho}\frac{\partial p}{\partial r} = \frac{\omega_0^2R^4}{r^3}. \]
Now, let the fluid surface be given by $z = f(r)$. At the free surface the pressure is fixed (to be the ambient atmospheric pressure), so $\frac{d}{dr} p(r,f(r)) = 0$. From the chain rule this implies \[ \frac{\omega_0^2R^4}{r^3} - g f'(r) = 0\] which shows that the fluid depth dips by \[ f(r) = f(R) + \frac{\omega_0^2R^2}{2g} - \frac{\omega_0^2R^4}{2g r^2}. \] Presumably, where $f(r)$ drops below zero is inside the drain hole.
Forced vortex
For the second problem of the forced rotation, I'd like to present a slightly different method of computation. The physical model of this problem is to set a bucket of water spinning around the central axis of the bucket. Now, in the idealized perfect fluid, the lack of interaction between concentric layers means that any work done spinning the bucket will not be transferred to the fluid. However, we are interested in the steady state problem. In the steady state the fluid will be co-rotating with the bucket and each concentric layer will have the same angular velocity (so there's non-vanishing vorticity and the framework of the previous problem cannot be used), so there is no shear. In the regime where there is no shear, viscosity plays no role. So after the fluid has settled down to a steady state, we can analyse it as if it were incompressible and inviscid.
For this problem in particular, we can use the action principle. In the steady state, the total kinetic energy of the fluid is given by \[ T = \int_0^R \pi \rho f(r) r^3 \omega_0^2 dr \] where the factor of $\pi$ enters from the suppressed azimuthal integral, and the computation comes from the particulate $\frac{1}{2} mv^2$ expression for kinetic energy. The function $f(r)$ is, as before, the height of the fluid. The potential energy is gravitational \[ V = \int_0^R \pi f(r)^2 g r dr\] The incompressibility gives the volume constraint that $\int f(r) r dr$ is a fixed constant. In the steady state the action principle gives that $S[f] = T - V$. To compute the variation, observe that the volume constraint implies $\int \delta f(r) r dr = 0$, and so by fundamental theorem of calculus, the admissible perturbations are such that \[ \delta f(r) = \frac{1}{r} \frac{d}{dr} \delta h(r) \] where \[ h(R) = h(0) = 0. \] Thus we can compute $\delta S[f]$ and integrate by parts to obtain the Euler-Lagrange equation \[ \frac{d}{dr}(r^2\omega^2 - 2f(r) g) = 0 \] which leads to the paraboloid solution \[ f(r) = f(0) + \frac{r^2\omega^2}{2g}. \]
(I have a bit of fondness for this problem as it appeared on the 2001 International Physics Olympiad's experimental section. We were then to use the parabolic surface of the spinning bucket of gel as a focusing mirror.)
How to ballast your boat
So far the discussion is fairly well-known. Now let us consider a floating body on the vortex. We'll assume that the angular motion of the floating body is driven by the fluid's rotation, so that at every point of its journey its angular speed is equal to that of the fluid's.
We try to draw a force diagram for the object. It experiences the force of gravity and the centrifugal force at its centre of mass. The force of gravity is $mg$ and the centrifugal force is $mv^2 / r$: in the case of a maelstrom, it is $m\omega_0^2 R^4 / r^3$, and in the case of the forced vortex it is $m\omega_0^2 r$.
On the other hand, it also experiences a force due to the pressure of the water at its centre of buoyancy. By Archimede's principle, this force is equal and opposite to the sum of the gravitational force and the centrifugal force on the water displaced. We can assume that the total net force normal to the water surface is zero, and we examine the radial drift of the floating body.
If the radial position of the centres of mass and of buoyancy are equal, then the total force on the object must be zero, so the object stays with the current and rotates around the vortex. This is the case of the ship being perfectly ballasted.
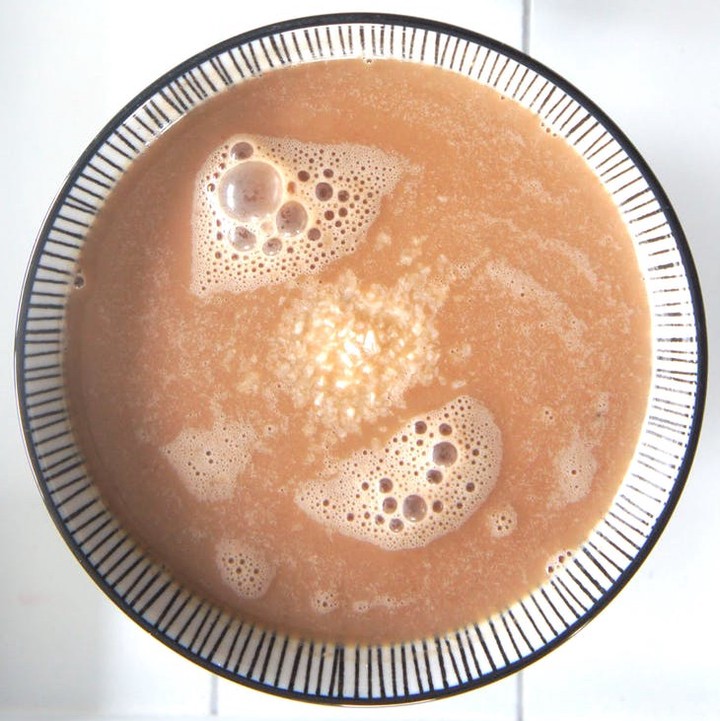
If the centre of mass is shallower than the centre of buoyancy (say, of a beach ball floating on water, or any uniform, lighter-than-water body), then we see that the radial position of the centre of mass $r_m \le r_b$ the radial position of the centre of buoyancy. In a forced vortex, this means that the force of buoyancy provided by the water pressure in the radial direction $\omega_0^2 r_b \ge \omega_0^2 r_m$ the centripetal force required to keep the object on that circular trajectory, so the under-ballasted ship will drift toward the centre of a forced vortex. This should be familiar for those people who have stirred powdered milk or made hot chocolate: when the mug or pot is stirred, the floating clumps of powder congregates toward the centre. On the other hand, in a free vortex, the force of buoyancy in the radial direction is $\omega_0^2 R^4 / r_b^3 \le \omega_0^2 R^4 / r_m^3$ the requisite centripetal force, so objects will drift away from the vortex! This explains why, after washing dishes and pulling drain-stop, the floating food bits tend not to go down the drain but end up stuck to the walls of the kitchen sink.
We can also consider over-ballasted ships. This tend to be the norm to ensure stability for travel at sea, especially in face of changing barometric pressures. Now the centre of mass is deeper than the centre of buoyancy $r_m \ge r_b$, and we see that the conclusions are reversed! For a forced vortex the over-ballasted ship will be turned away from the vortex, whereas in a maelstrom the over-ballasted ship will be sucked in!
So the moral of the story is: if your ship is trapped in a maelstrom, throw all ballasts overboard and stand up straight holding your arm over your head, and hope for the best.