Whitney Extension and Counterexample to Sard's Theorem

2012-11-21 Last updated on 2019-06-27 9 min read expository

Whitney's construction.

In a first course in differential geometry/topology we are often taught the following version of Sard's theorem:

Theorem [Sard, smooth case]

Let $M$ and $N$ be (finite dimensional) smooth manifolds, and let $f:M\to N$ be a smooth (infinitely differentiable) map. Let $S\subset N$ be the set of critical values, that is, for every $y \in S$ there exists $x \in f^{-1}(y)$ such that $f'(x)$ is not surjective. Then $S$ has measure zero.

It turns out that Sard in his 1942 paper proved something stronger.

Theorem [Sard]

Let $f:\mathbb{R}^m \supset M\to N\subset \mathbb{R}^n$ be a mapping of class $C^k$ (all partial derivatives up to order $k$ exists and are continuous) for $k \geq 1$. Let $S\subset N$ be defined as above. And if either

$m \leq n$; or
$m > n$ and $k \geq m - n + 1$,

then $S$ has measure 0.

Over at MathOverflow, Sergei Ivanov has shown that in the case $m = n = 1$, the statement can be modified so that $C^1$ is not necessary.

In this post, we will describe counterexamples in the cases $m > n$ if the condition on $k$ is not satisfied. We will also sketch a natural generalisation of Ivanov's argument for higher dimensions.

Extremely degenerate critical points

The argument given by Ivanov was implicitly contained in Sard's original 1942 paper. It contains the following observation based on Taylor's Theorem:

Observation

Let $f:\mathbb{R}^m \to \mathbb{R}^n$ be a function such that $f(0) = 0$. If $f$ is $k$-times differentiable at the origin with the first $k$ derivatives vanishing, we have $|f(x)| = o(|x|^k)$ as $x\to 0$.

In particular, for each $\epsilon > 0$ there exists a $\delta$-neighborhood of the origin such that \[ |f(B_\delta)| \leq \sup_{x\in B_\delta} |2 f(x)|^n \leq \epsilon |x|^{kn}.\]

Now we prove

Theorem

Let $f:\mathbb{R}^m\supset M \to \mathbb{R}^n$ be a function where the domain $M$ is open and has finite measure. Let $S'\subset \mathbb{R}^n$ be such that for every $y$ in $S'$, there exists $x\in f^{-1}(y)$ such that the first $k$ derivatives of $f$ exists and vanishes at $x$, where $k \geq \frac{m}{n}$. Then $S'$ has measure 0.

Proof:

By the observation above, given $\epsilon > 0$ we have that for every $y\in S'$ there exists a ball $B(y)\subset 5B(y) \subset M$ such each $B(y)$ has measure at most one and the measure $|f(5B(y))| \leq \epsilon |B(y)|^{kn/m}$. Applying the Vitali covering lemma we can find a countable subcollection $\{B_i\} \subset \{B(y)\}$ such that $\cup_i 5B_i \supset \cup_{y\in S'} B(y)$ and that the $B_i$ are pairwise disjoint. This implies \[ |f(S')| \leq |\cup_{y\in S'}f(B(y))| \leq |\cup_i f(5B_i)| \leq \epsilon \sum_i |B_i|^{kn/m} \leq \epsilon \sum_i |B_i| \leq \epsilon |M| \] where in the 4th inequality we used that $kn/m \geq 1$ and $\sup_i |B_i| \leq 1$ and in the last inequality we used that $B_i$ are disjoint subsets of $M$. Taking $\epsilon \to 0$ we get the desired conclusion.

Ivanov's argument is the special case $m = n = k = 1$. Note that we did not assume that $f$ is $C^k$; we merely assumed $k$ times differentiability (and the vanishing of the top $k$ derivatives at the "critical" points.

Low regularity counterexample

The counterexample to Sard's theorem when $k$ is too small was already constructed by Hassler Whitney 7 years prior¹. It is an interesting application of the Whitney extension theorem.

Theorem [Whitney extension]

Let $A \subset \mathbb{R}^m$ be a closed set. Let $f_\alpha:A \to\mathbb{R}$ be a family of functions for every multi-index $|\alpha| \leq k$ for some natural number $k$, such that the $f_\alpha$ are compatible as possible Taylor expansions of some $C^k$ function (see the Wikipedia entry for a more precise formulation), then there exists a function $f:\mathbb{R}^m\to\mathbb{R}$ that is class $C^k$ (and in fact real analytic outside of $A$) such that it and its derivatives up to order $k$ coincide with $f_\alpha$ on the set $A$.

In view of the extension theorem, to construct a counterexample to Sard's theorem in dimensions $m = 2, n = 1, k = 1$ it suffices to construct a closed subset $A$ of $\mathbb{R}^2$ on which $f$ is non-constant but is compatible with having vanishing partial derivatives everywhere. (That this is possible is due to the fact that along non-rectifiable curves, the value of $f$ at two points cannot necessarily be represented by "an integral of the derivative".)

To be more precise, it suffices that we construct a set $A\subset \mathbb{R}^2$ and a function $f:A \to\mathbb{R}$ such that

$A$ is closed
$f(A)$ has positive measure
for $x,x'\in A$ we have that $|f(x) - f(x')| = o(|x - x'|)$

The third condition ensures that the function $f$ is compatible with having vanishing derivatives everywhere along $A$. Note that the Whitney extension of such a function $f$ would necessarily have the set $S$ containing $f(A)$, which has positive measure.

As with often the case, the construction of $A$ and $f$ relies on a self-similar procedure that is familiar from fractal constructions. Indeed, a self-similar construction allows for $|f(x) - f(x')|$ and $|x - x'|$ to scale differently, which is also behind such constructions as the Cantor staircase.

We start by taking the unit square and removing four smaller squares from it, each of the four squares have side length $\alpha$. On the remaining set we draw line segments connecting the midpoints of the squares as shown in red. This gives our construction at step 1. We iterate now inside each of the small squares by taking a copy of the step 1 construction, scaling it by $\alpha$, and pasting it inside so the path connects. We show the procedure for one of the small squares in blue.

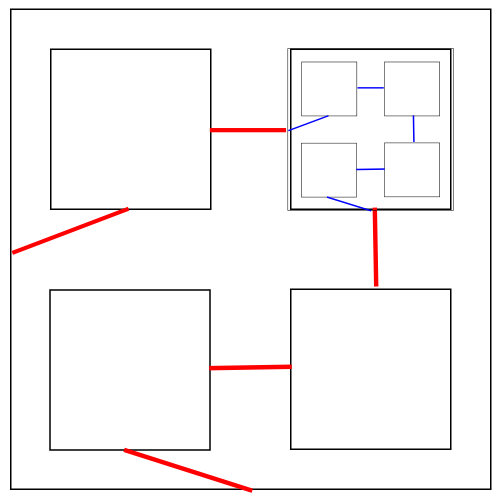
Whitney's construction illustrated: starts with a unit square from which four smaller squares are removed, and a partial path is drawn. By iteration we fill each smaller square with a scaled and rotated/reflected copy of the original one.

The set $A$ will consist of the closure of the union of the red paths with all of its scaled copies. It is clear that this is a closed, connected set that is topologically identical to the closed unit interval. We explicitly parametrise the set $A$ as follows: divide the unit interval into nine equal portions. The odd numbered portions correspond to the red parts in the image above. The even numbered portions correspond to the portions within the small squares. Each of the even numbered portions we divide into nine parts and repeat. In other words, we use a construction similar to the Cantor staircase. Express the numbers in the interval $[0,1]$ in base 9. Let $p:(0,1)\to \mathbb{N}\cup \infty$ be the function that assigns to a number $s$ the position (after the "decimal" point) in base nine of the first appearance of a even "digit". So $p(0.21345\ldots_9) = 1$, and $p(0.1357802\ldots_9) = 5$. Then we can conclude that $x$ belongs to one of the line segments added at the $p(x)$th step of the construction if $p(x)$ is finite. The points where $p(x)$ are infinite are the limit points added during the closure.

To define $f$ on $A$, first we send $f(0) = 0$ and $f(1) = 1$. For $x\in (0,1)$, we consider its base-9 expansion and truncate it after the first even digit. So $0.13572841\ldots_9 \mapsto 0.13572$. Now that the remaining digits are all odd except the last, we replace them by the rule $n \mapsto (n-1)/2$; the last digit we replace by $n\mapsto n/2$. So that $0.13572 \mapsto 0.01231$. This last number we interpret in base-4 (where $0.\cdots \beta 4_4 = 0.\cdots (\beta+1)_4$ by convention), which we regard as the value of $f(x)$. So as a function on $[0,1]$, the construction of $f$ is exactly analogous to the Cantor staircase function, and is uniformly continuous but not absolutely continuous. It is almost everywhere constant and not differentiable at the "limit points" when considered as a function on $[0,1]$. On the other hand, its differentiability property improves when considered as a function on $A$, because of the change of scale built into the construction.

We see immediately on each of the line segments $f$ is constant. Furthermore, a bit more reflection shows that if $\ell$ and $\ell'$ are two line segments of $A$ which touch each other, we have that $f(\ell) = f(\ell')$. This implies that if $x\neq x'$ are such that $f(x)\neq f(x')$, either (a) at least one of $x,x'$ has $p$ that is infinite, or (b) there is some $x_0$ between them with $p(x_0) = \infty$. If $x, x'$ in base-9 expansion differs at the $j$th digit, the difference of their base-9 expansions must be strictly greater than $9^{-j-1}$. Or, in other words, after the $j+1$th stage of the construction of $A$, the two points must be separated by one whole step. This means that the planar distance $|x-x'|$ scales like $\alpha^{j}$. On the other hand the difference $|f(x) - f(x')|$ scales like $4^{-j}$, hence we have that $|f(x) - f(x')| = O(|x - x'|^{\log_\alpha 1/4})$. So if $\alpha$ is chosen to be $\alpha > 1/4$, we would have that $|f(x) - f(x')| = o(|x - x'|)$ as desired. (In Whitney's original paper, $\alpha$ is chosen to be exactly a third.)

Note that the "path length" of the set $A$ is precisely $r\sum_j (4\alpha)^j$ where $r$ is the total length of the red segments in the image above. We see that when $\alpha < \frac14$ the path length is finite. This means that $A$ represents a rectifiable path and hence we can express $f$ as an integral of its derivatives along $A$, and hence the desired property is not possible. (Or, in other words, we cannot "cancel" the singularity in the Cantor staircase with singularities in the embedding [as there are none].) When $\alpha > \frac14$ we see that "path length" diverges strongly. This non-rectifiability is what allows us to finish this construction.

Lastly, as a sanity check, we can make sure that $f$ cannot be extended to a $C^2$ function with first derivative vanishing everywhere along $A$. Were that to be possible we need $|f(x) - f(x')| = o(|x - x'|^2)$. From the construction above we see that this requires $\alpha^2 > 1/4$. But to fit four identical squares into a bigger one we need necessarily $\alpha < 1/2$, and so $C^2$ is not possible, in agreement with Sard's theorem.

Whitney's original paper can be found here. ^{^}

math.CA

Willie WY Wong

Associate Professor

My research interests include partial differential equations, geometric analysis, fluid dynamics, and general relativity.

Whitney Extension and Counterexample to Sard's Theorem

Extremely degenerate critical points

Low regularity counterexample

Whitney's construction illustrated: starts with a unit square from which four smaller squares are removed, and a partial path is drawn. By iteration we fill each smaller square with a scaled and rotated/reflected copy of the original one.

Willie WY Wong

Associate Professor

Related